Alexandre V. Boukalov
e-mail: boukalov@gmail.com
The Centre of Physical and Space Researches, International Institute of Socionics
"Physics of Consciousness and Life, Cosmology and Astrophysics" journal, issue
2, 2001
.
Thinking and quantum physics:
the Gödel and Tarski theorems and uncertainty principle
It is shown that the quantum-mechanical regularities of thinking found their reflection in the metamathematical paradoxes and they are expressed by the Gödel and Tarski theorems. It is proposed the uncertainty relation for formal and semantic describing of the objects in metamathematics, and also an explanation of the “paradox of a liar”. The obtained results can be used in creation of artificial intelligence on the base of quantum computers.
Key words:
quantum mechanics, quantum-mechanical thinking, metamathematical paradoxes, formal-semantic uncertainty relation, artificial intelligence, quantum computer.
If the thinking regularities are like to the quantum-mechanical ones [1], it means that the uncertainty principle must appear also in the mathematical thinking field. Really, in the mathematics part which deals with the mathematics grounds analysis, there is the Tarski theorem for the uncertainty principle in mathematical logic. If the A theory is uncontradictory then the dialogical function D and the sets U of the all true propositions of the A theory cannot be simultaneously determined in A [5]. Here D is the function of the statement numeration in the A model. It is the formulae function and it expresses the formal aspect in the A theory. The set of all true statements of the A theory shows this theory semantics. Thus the formal and semantic descriptions of the A theory are simultaneously undetermined and additional. Thus it is risen the two cases, considered in mathematics: either in the uncontradictory theory the dialogical function D is determined whereas the set of its truth statements U is undetermined, or the function D is undetermined under the U determination. If one compares the operator 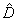 Āto the D one and the operator
Āto the D one and the operator  Āto the U one, then we are able to obtain the expression, connected with the uncommunication of these functions or operators:
Āto the U one, then we are able to obtain the expression, connected with the uncommunication of these functions or operators:
![]() (1)
(1)
Correspondingly, if we do not consider, as above, the confluent cases and introduce some measures m(D) and m(U) of the functions D and U spaces, we are able to write the analogy of the physical uncertainty relation in mathematics:
ΔD·ΔU ≥ z (2)
where ΔD and ΔU are the measures of the D and U deviations from the true values. The errors of the D and U quantities determination cannot be less than some constants in the A theory. It means that the error of the simultaneous measuring (or calculation) ΔD and ΔU cannot be less than the constant z. Thus we can formulate the theorem:
Theorem: In the probability sense under the presence of the inaccuracies (or uncertainties) D and U can be simultaneously determined in A[1].
Thus the formal description of the theory has no true or semantic contents whereas in the case of the semantically true theory there is no formalized description despite its possible complexity. It is correct for many parts of mathematics including the recursive arithmetic, which is the base for the quantum theory. In the considered presentation the quantum mechanics uncertainty principle is formulated by the following way:
Under the energetical quanted (numerical) description the quantum-mechanical theory or system is unsolved in the coordinate presentation (coordinate is not determined, i.e. it is absent or determined with the significant error). The opposite is truthful: under the whole space-time description the theory is unsolved in the momentum-energetical presentation.
Really, if we consider the formal objects, including the logical ones, as the consciousness objects, the observation property (under the consciousness unobservation) and also their discreteness and finiteness (language, symbol, expressions), we are able to compare them as the formal, observed, discreteness objects with the quanted energy-momentum.
Thus the formal operator 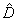 Āis analogous to the quantum-mechanical momentum operator
Āis analogous to the quantum-mechanical momentum operator 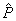 . Then the semantic operator
. Then the semantic operator  Ācan be compared to the coordinate operator
Ācan be compared to the coordinate operator 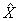 . Under this presentation the space-time uncertainty analogy ΔX is the uncertainty of the sense ΔU. As a result we can present the comparison of the two notions in mathematics and quantum mechanics.
. Under this presentation the space-time uncertainty analogy ΔX is the uncertainty of the sense ΔU. As a result we can present the comparison of the two notions in mathematics and quantum mechanics.
| mathematics | quantum mechanics |
| If a theory is formal by its sense it has no contents. | The precise observation of momentum eliminates the knowledge of the coordinate or the motion trajectory ΔX of the particle. |
| The pithy theory is not formalized. | The coordinate observation eliminates the interference and the momentum value ΔP. |
| ΔD·ΔU≥z | ΔP·ΔX≥ħ/2 |
It is obvious that the Gödel incompleteness theorem can be interpreted by the same sense:
The Gödel incompleteness theorem:
Every logical system, rather rich to include the arithmetic formalization, is either the ω-contradictive, or includes some unsolved (although a true one) formula, i.e. a one that in the given system it cannot be neither proved nor disproved (although with the use of additional means, which are beyond this system, it is possible to prove its truthness), by other words any given uncontradictive system of the mentioned type (syntactically and semantically) is uncomplete and even uncompletable [5].
Thus this theorem proves the principal inexpressibility of impossibility of verbalization (i.e. unobservation) of mathematical objects (or the objects of the mathematical thinking as well as other any one). It is interesting to note that Gödel, under the theorem proof, used the liar paradox (somebody says: “I lieģ”). But this statement can be extended till the gradation of the expression shades, i.e. to introduce some measure, what reveals the possibility of the distinction between the phenomenon and semantic aspects of statement and eliminates the paradox:
a) The more formally one says ōI lieö the more semantically he says truth. Thus the formal aspect of the formula states the statement which itself is true and uncontradictable, i. e. it is internally semantically true, but contentsless.
b) The more this phrase is true in semantic, contents, truth aspect, the less it is true formally, i.e. it cannot be joined to the formal statements set. Thus it is risen the two cases:
1) 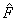 (I lie) is definable and
(I lie) is definable and 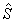 (I lie) is indefinable;
(I lie) is indefinable;
2) 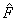 (I lie) is indefinable and
(I lie) is indefinable and 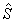 (I lie) is definable,
(I lie) is definable,
in dependence of what aspect, formal or semantic, we use for certain statement consideration.
In general case one can write: Δf(I lie)·Δs(I lie)>const. It is the formula for usual life expressions, where the two aspects[2] are present in the mixed form, which ate distincted by the human reason but not by a device.
Let us note, that this relation has a partial case which is the Lofti-Zade theory of illegible sets, which operates by the illegible determined notions. By this sense it differs from the whole theory in such a way as the description of the reduced wave function in quantum mechanics (what gives the probabilities distribution) differs from the unreduced (what gives the interference and superposition of the probability amplitudes of the formal and semantic aspects). We can take into account the vector of state of the thinking wave function ψB(f,s), including the two additional aspects, and the operators 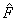 ,
, 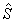 , acting on this wave function. Note, the more simple is a formal proposition, the more values it includes[3].
, acting on this wave function. Note, the more simple is a formal proposition, the more values it includes[3].
Under such consideration for the wave function ψB(f,s) = 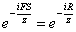 Ā(where R is an analogy of momentum), the following quantum-mechanical equations can be written:
Ā(where R is an analogy of momentum), the following quantum-mechanical equations can be written:
![]() (3)
(3)
From this point of view the human perception of integer numbers and the skillness of these numbers operation can be a reflection of the quantum cells of the thinking phase space, whereas the mentioned cells are determined by the Planck constant ħ or its analogy z.
If we use the quantum mechanics formulation, proposed by R.Feynman in the form of integrals over trajectories, it is possible to consider the integrals in the formal, sign and semantic, sense space.
Thus, the logical sentiments can be presented as the motion in the formal space of alternative trajectories[4]. In opposite, the motion in the semantic space of alternative trajectories is the intuitive cognition process[5]. Under this process the observation by the consciousness of some internal (psychical) constructions or images can be described by the formalism of the M.Mensky complex Hamiltonian function [6].
The Gödel and Tarski theorems are connected mutually. It is noted in [3, 5], whereas the Gödel theorem shows the principal limitation of any rather rich system, the Tarski theorem shows the limitation of the expression possibilities of such systems.
If we take into account the above mentioned suppositions and use them for the quantum mechanics analyses, we can reveal the following. Firstly, the quantum mechanics is uncompleted principally as a system. In particularly it assumes, according to the Gödel theorem, the unproved suppositions about the covered variables existence.
The similar models within the orthodox quantum mechanics were proposed by L. de Broglie, J.P.Vigier, D.Bohm at al. Within the improved quantum mechanics system, proposed by us [2], these models are true as the phenomenological ones. Secondly, the expression possibilities limitation (due to the Tarski theorem) of the orthodoxal quantum mechanics is determined by the Heisenberg uncertainty principle (or the Bohr complementarity principle). The similar consideration can be produced also for others physical theories. For example, the classical mechanics can be completely formalized by the refusal of the processes consideration in the nonuniformal unconfluent Newtonian space-time. H. Poincaré showed [4] that we consider either the forces, acting on the classical mechanics objects, or the space geometry, where these objects move. This complementarity also, maybe, corresponds to the Tarski theorem: the space geometry determines the set of the true objects motions.
Thus the usage of the connection of the Gödel and Tarski theorem with the uncertainty principle provides us to spread beyond the existing theoretical schemes[6] in order of their improvement, generalization and the cognition limits extension. The understanding of the thinking paradoxes origination provides the more directed reconstruction of the mathematics grounds. Besides the considered problems have the direct relation to the development and functioning of the artificial intellect, its skill to perceive the senses and to operate by them and not only by formal constructions. In the artificial intellect, which can be developed on the base of the quantum computers, the mentioned regularities will be revealed inevitable. And the formalized programming will be insufficient without the semantic training. Without the correspondent training the semantic knowledge of artificial intellect can be formed by occasional cases and thus its behaviour can be rather unpredictable due to the action of the formal semantic uncertainty relation (2).
References:
- Boukalov A.V. Psychics, living processes and quantum mechanics Ś a phenomenological approach. // Physics of consciousness and life, Cosmology and Astrophysics. Ś 2001. Ś N 1. Ś P. 22¢32.
- Boukalov A.V. // Physics of consciousness and life, Cosmology and Astrophysics. Ś in press.
- Kleene S.C. Mathematical logic. Ś New York , London, Sydney: John Wiley & Sons Inc. 1967.
- Poincaré H. Science et métode. Ś Paris, 1908.
- Fraenkel A.A., Bar-Hillel Ye. Foundation of set theory. Ś Amsterdam: North-Holland Publishing Company, 1958.
- Mensky M.B. Quantum Measurement and Decoherence: Models and Phenomenology. Ś Dordrecht: Kluwer Academic Publ., 2000.
Main page | About journal
Copyright © 2001-2007 International Institute of Socionics
Design by Olga Karpenko